Grasshopperからfortranやmatlabなどの外部の実行ファイルを呼び出して、
データ入力⇒演算⇒結果取得を行うフローの紹介です。
既存のソルバープログラムや計算エンジンを流用し、プリ・ポスト処理のみRhino・Grasshopperをビジュアルツールとして活用できます。
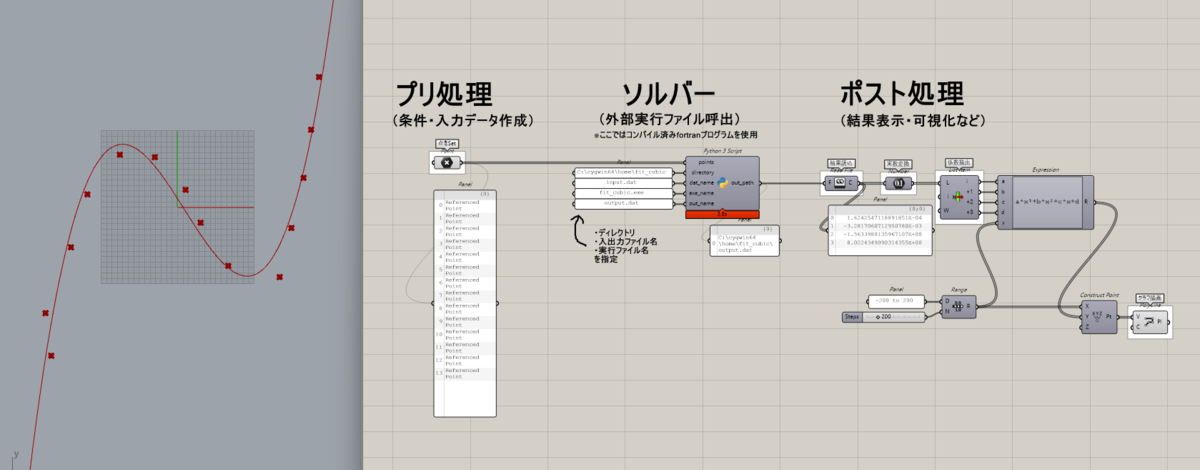
ここでは、サンプルとして、
①プリ処理:Rhinoで点を複数適当に作る
②計算処理:それらにフィットする近似三次曲線の係数を最小二乗法プログラム(fortran)で求める
③ポスト処理:計算結果をGrasshopperに読み込み、三次曲線を描画
ということをやってみます。
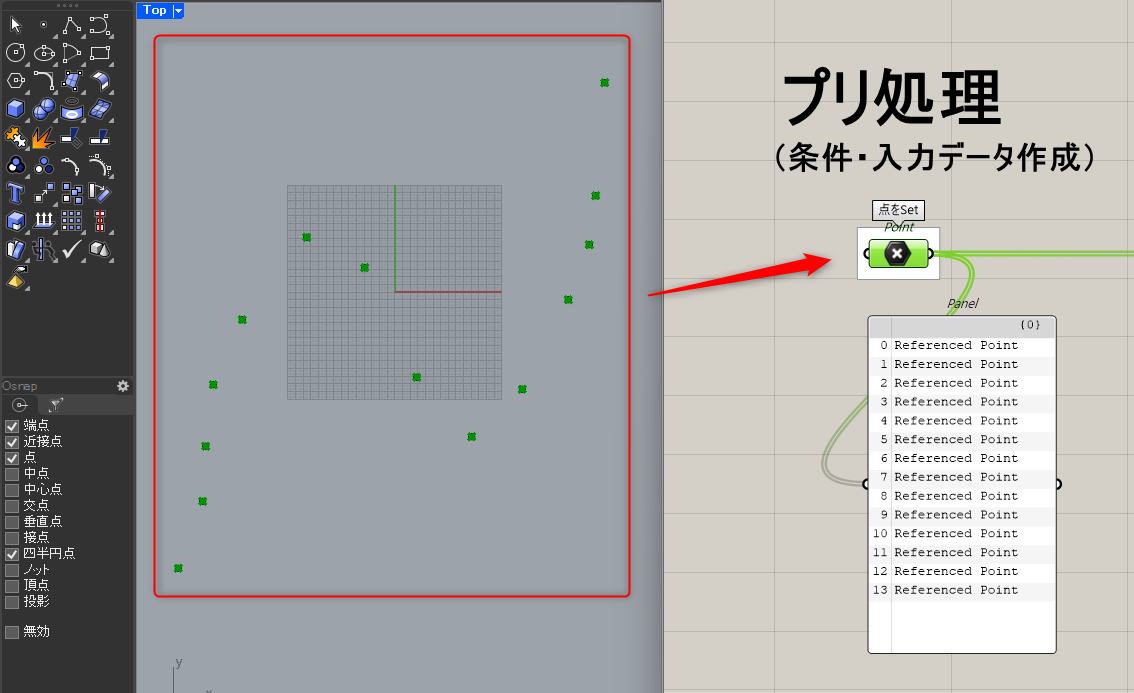
①プリ処理(Pre-Process)
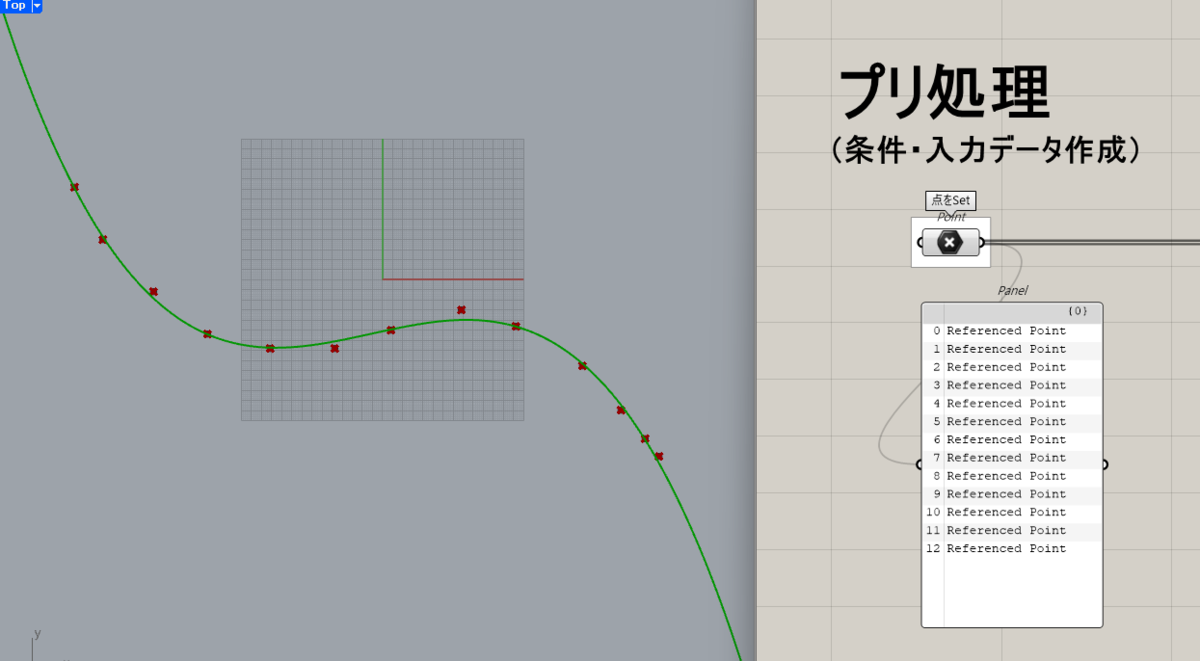
Rhinoで作成した点オブジェクトをGrasshopperの[Point]コンポーネントに「右クリック>Set Multiple Points」でSetします。
構造解析の場合は、梁の曲線や節点の点、
流体解析の場合は、境界条件やパラメータ、
など、それぞれの演算や解析手法に置き換えて入力するものをイメージしてみてください。
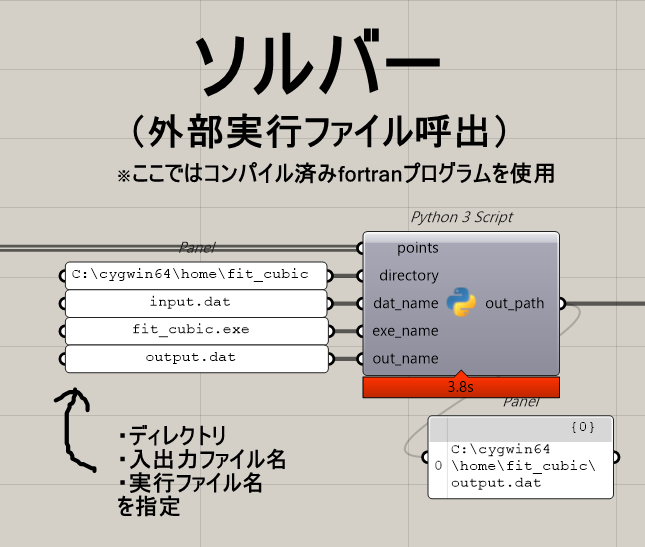
②計算処理(Solver)
①の点にフィットする近似三次曲線の係数を最小二乗法プログラム(fortran)で求めます。
fortranプログラムは予めコンパイルして実行ファイル形式にしておき、指定したディレクトリに置いておきます。
呼び出し部分は[python 3]コンポーネントで記述しています。
実行ファイル形式で、pythonのsubprocess.runで呼び出せれば良いので、fortranに限らず、言語はmatlabでもC++でも応用可能です。
ここでは、一旦入力データを「input.dat」として指定フォルダに書き出し、それをexeファイルに入力するようにしています。必要最低限しか記述していないので、例外処理を入れたり、スイッチをつけたり、エラーログを出力するようにしたりすればもっと使いやすくなると思います。
(使用した最小二乗法プログラムのソースコードはページ末尾参照)
<Python 3 Scriptの中身>
import os
import subprocess
# Inputファイル生成
dat_path = os.path.join(directory, dat_name)
with open(dat_path, "w", encoding="utf-8") as f:
for (x, y, z) in points:
f.write(f"{x},{y},{z}\n")
# Exe実行
exe_path = os.path.join(directory, exe_name)
result = subprocess.run([exe_path], cwd=directory, capture_output=True, text=True)
# Outputファイルパス出力
out_path = os.path.join(directory, out_name)③ポスト処理(Post-Process)
②で計算した結果は「output.dat」として同じディレクトリに書き出すプログラムになっているので、それをGrasshopperに[Read file]コンポーネントで読み込みます。
読み込んだデータは[Number]で実数変換し、それぞれの係数を[List item]で取り出して[Expression]で各Y成分を計算して[Construct Point]+[Polyline]でビューに描画します。
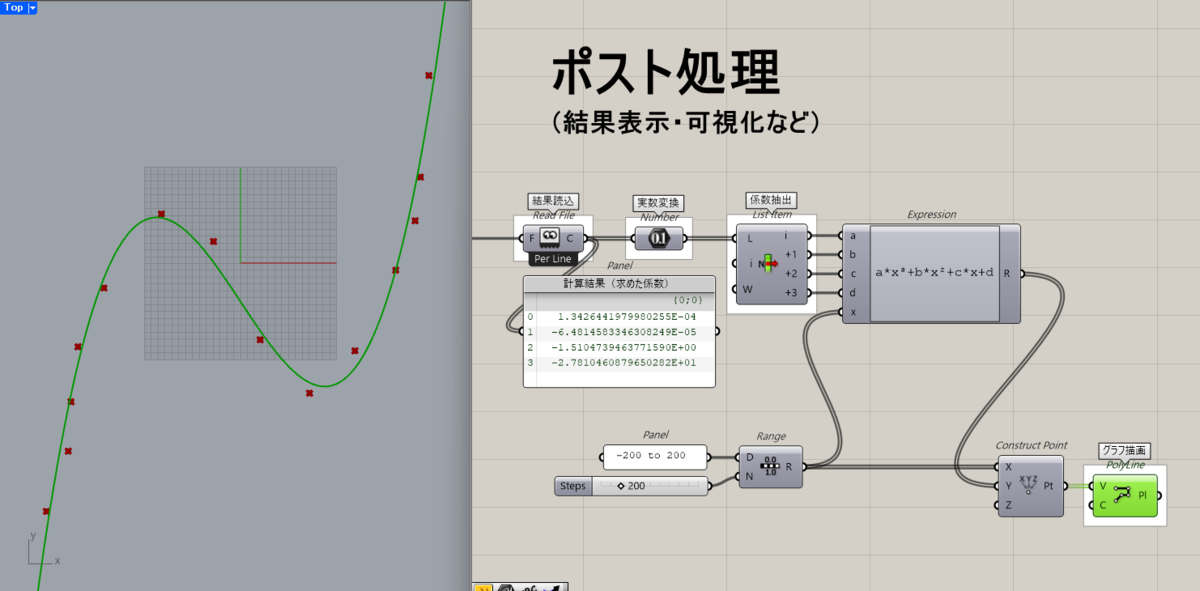
入力する点をSetし直せば、リアルタイムに反映されます。
このポスト処理部分も、
構造計算の場合は、応力や変位の分布、各種グラフの出力、
流体解析の場合は、流量や流速ベクトルの分布、各種グラフの出力、
など、それぞれの演算や解析手法に置き換えて可視化するものをイメージしてみてください。
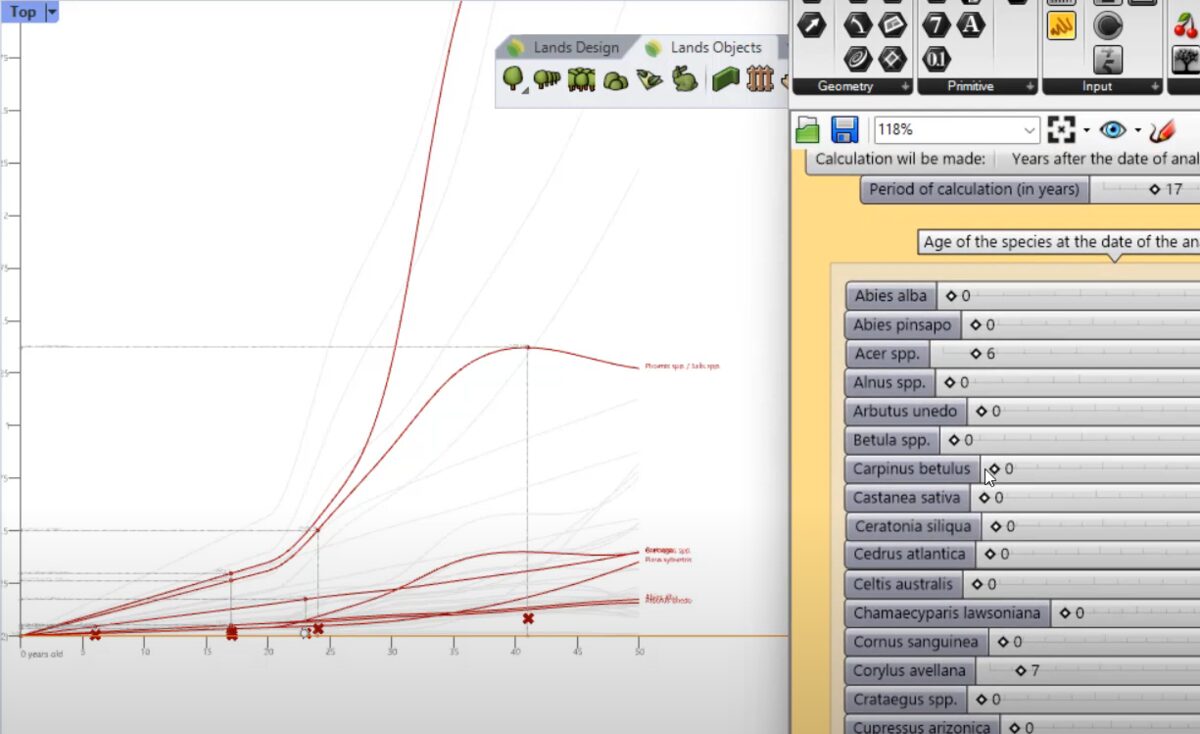
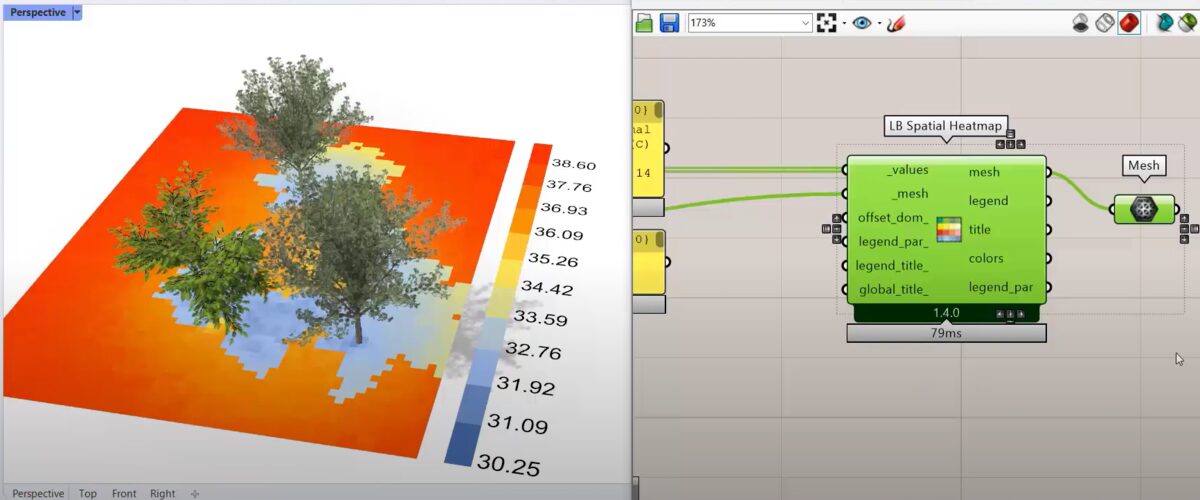
以下は、計算自体も外部ファイルではなくGrasshopper内で行っているものですが、Grasshopperを使ってグラフやカラーマッピングをRhinoのビューに描画した例です。
Grasshopperでは、コンポーネントと呼ばれるノードを線で繋ぐ方法(ビジュアルプログラミング、ノードベースプログラミング)で2次元・3次元のモデリングやグラフィックに関するプログラムの作成が可能です。
まとめ
Rhino・Grasshopperは、ある意味「3Dビューワ付きプログラム実行環境」のようなものですので、データを作ったり、取り込んだりして、それを自動で可視化、見える化することは大得意です。
もちろんC#やPythonで書き直せばすべてGrasshopper内で直接計算して完結できるのですが、既存コードを書き直すのもデバッグやテストも含め工数がかかるので、そのまま使えると便利という方もいるのではないかと思います。
- 開発済みのコードやプログラムを別の言語に書き換えずそのまま利用したい
- 入力や可視化のプログラムを実装する方法を探している
- 入力データはテキストベースで作成しているから正しく入力できているか不安、しっかり2次元・3次元でグラフィカルにプレビューしながら入力データを作成したい
- 計算結果を綺麗で正確なグラフや図として自動出力したい
というような方は是非参考にしてみてください!
(参考)使用した最小二乗法プログラムソースコード(fortan)
! fit_cubic.f90
! 最小二乗法で y = a x^3 + b x^2 + c x + d を近似
! 入力: input.dat (各行: x,y,z ※カンマ区切り)
! 出力: output.dat
program fit_cubic
implicit none
integer, parameter :: dp = selected_real_kind(15, 300)
character(len=512) :: line
real(dp) :: x, y, z
integer :: ios, n
! 各種総和(正規方程式用)
real(dp) :: sx0, sx1, sx2, sx3, sx4, sx5, sx6
real(dp) :: syx0, syx1, syx2, syx3
! 4x4の係数行列と右辺、解(a,b,c,d)
real(dp) :: A(4,4), bvec(4), coeff(4)
! 初期化
sx0 = 0.0_dp; sx1 = 0.0_dp; sx2 = 0.0_dp; sx3 = 0.0_dp
sx4 = 0.0_dp; sx5 = 0.0_dp; sx6 = 0.0_dp
syx0 = 0.0_dp; syx1 = 0.0_dp; syx2 = 0.0_dp; syx3 = 0.0_dp
n = 0
! 入力ファイルを開く
open(unit=10, file='input.dat', status='old', action='read')
do
read(10,'(A)', iostat=ios) line
if (ios /= 0) exit ! EOF or error -> ループ脱出
if (len_trim(line) == 0) cycle ! 空行スキップ
read(line,*, iostat=ios) x, y, z
if (ios /= 0) cycle ! ヘッダ行などは読み飛ばし
! 累積和更新
sx0 = sx0 + 1.0_dp
sx1 = sx1 + x
sx2 = sx2 + x*x
sx3 = sx3 + x*x*x
sx4 = sx4 + x*x*x*x
sx5 = sx5 + x*x*x*x*x
sx6 = sx6 + x*x*x*x*x*x
syx0 = syx0 + y
syx1 = syx1 + y*x
syx2 = syx2 + y*x*x
syx3 = syx3 + y*x*x*x
n = n + 1
end do
close(10)
if (n < 4) then
print *, 'データ点が4点未満のため三次多項式を当てはめできません。'
stop 1
end if
! 正規方程式(X^T X * coeff = X^T y)を構築
! 列順: [x^3, x^2, x, 1] に対応して coeff = [a,b,c,d]
A = reshape([ &
sx6, sx5, sx4, sx3, &
sx5, sx4, sx3, sx2, &
sx4, sx3, sx2, sx1, &
sx3, sx2, sx1, sx0 &
], shape(A))
bvec = [ syx3, syx2, syx1, syx0 ]
call solve_4x4(A, bvec, coeff)
! 出力
open(unit=20, file='output.dat', status='replace', action='write')
write(20,'(ES25.16)') coeff(1)
write(20,'(ES25.16)') coeff(2)
write(20,'(ES25.16)') coeff(3)
write(20,'(ES25.16)') coeff(4)
close(20)
print '(A,1x,ES16.8,1x,ES16.8,1x,ES16.8,1x,ES16.8)', 'a b c d =', coeff(1), coeff(2), coeff(3), coeff(4)
print *, 'output.dat に係数を書き出しました。'
contains
! 4x4連立一次方程式 A x = b を部分ピボット付きガウス消去で解く
subroutine solve_4x4(A, b, x)
real(dp), intent(inout) :: A(4,4)
real(dp), intent(inout) :: b(4)
real(dp), intent(out) :: x(4)
integer :: i, j, k, p
real(dp) :: maxval, tmp, factor
! 前進消去
do k = 1, 4
! ピボット選択(列kで最大の行を探す)
p = k
maxval = abs(A(k,k))
do i = k+1, 4
if (abs(A(i,k)) > maxval) then
maxval = abs(A(i,k))
p = i
end if
end do
if (maxval == 0.0_dp) then
print *, '警告: 行列が特異です(データの x が偏っている可能性)。'
stop 2
end if
! 行入れ替え
if (p /= k) then
do j = k, 4
tmp = A(k,j); A(k,j) = A(p,j); A(p,j) = tmp
end do
tmp = b(k); b(k) = b(p); b(p) = tmp
end if
! 正規化と消去
do i = k+1, 4
factor = A(i,k) / A(k,k)
A(i,k) = 0.0_dp
do j = k+1, 4
A(i,j) = A(i,j) - factor * A(k,j)
end do
b(i) = b(i) - factor * b(k)
end do
end do
! 後退代入
do i = 4, 1, -1
tmp = b(i)
do j = i+1, 4
tmp = tmp - A(i,j) * x(j)
end do
x(i) = tmp / A(i,i)
end do
end subroutine solve_4x4
end program fit_cubic
